optas.models.Model Class Reference

The Model base class. More...

Inheritance diagram for optas.models.Model:

Public Member Functions
def	__init__ (self, str name, int dim, List[int] time_derivs, str symbol, Dict[int, Tuple[List[float]]] dlim, Union[None, int] T)
	The Model base class initializer. More...
str	get_name (self)
	Return the name of the model. More...
str	state_name (self, int time_deriv)
	Return the state name. More...
str	state_parameter_name (self, int time_deriv)
	Return the parameter name. More...
str	state_optimized_name (self, int time_deriv)
	Return the sate optimized name. More...
Tuple[ArrayType]	get_limits (self, int time_deriv)
	Return the model limits. More...
cs.DM	in_limit (self, ArrayType x, int time_deriv)
	Check if array is within model limits. More...

Public Attributes
	name
	The name of the model. More...
	dim
	Model dimension. More...
	time_derivs
	Time derivatives required for the model. More...
	symbol
	A short symbol to represent the model. More...
	dlim
	Model limits. More...
	T
	Number of time steps. More...

Detailed Description

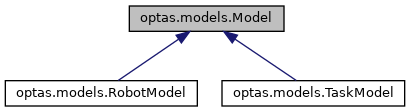
The Model base class.

Defines the base class utilized by all models.

Constructor & Destructor Documentation

__init__()

def optas.models.Model.__init__	(		self,
		str	name,
		int	dim,
		List[int]	time_derivs,
		str	symbol,
		Dict[int, Tuple[List[float]]]	dlim,
		Union[None, int]	T
	)

The Model base class initializer.

   @param name The name of the model.
   @param dim Model dimension (for robots this is ndof).
   @param time_derivs Time derivatives required for model, 0 means not time derivative, 1 means first derivative wrt to time is required, etc.
   @param symbol A short symbol to represent the model.
   @param dlim Limits on each time derivative, index should correspond to a time derivative (i.e. 0, 1, ...) and the value should be a tuple of two lists containing the lower and upper bounds.
   @param T Optionally use this to override the number of time-steps given in the OptimizationBuilder constructor.

   @return An instance of the Model class.

Member Function Documentation

get_limits()

Tuple[ArrayType] optas.models.Model.get_limits	(		self,
		int	time_deriv
	)

Return the model limits.

   @param time_deriv The time-deriviative required (i.e. position is 0, velocity is 1, etc.)
   @return lower The model lower limit.
   @return upper The model upper limit.

get_name()

str optas.models.Model.get_name

(

self

)

Return the name of the model.

   @return Name of the model.

in_limit()

cs.DM optas.models.Model.in_limit	(		self,
		ArrayType	x,
		int	time_deriv
	)

Check if array is within model limits.

   @param x The array containing values to be checked.
   @param time_deriv The time-deriviative required (i.e. position is 0, velocity is 1, etc.)
   @return Returns DM(1) if the array x is within the model limits, DM(0) otherwise.

state_name()

str optas.models.Model.state_name	(		self,
		int	time_deriv
	)

Return the state name.

   @param time_deriv The time-deriviative required (i.e. position is 0, velocity is 1, etc.)
   @return The state name in the form {name}/{d}{symbol}, where "name" is the model name, d is a string given by 'd'*time_deriv, and symbol is the symbol for the model state.

state_optimized_name()

str optas.models.Model.state_optimized_name	(		self,
		int	time_deriv
	)

Return the sate optimized name.

   @param time_deriv The time-deriviative required (i.e. position is 0, velocity is 1, etc.)
   @return The parameter name in the form {name}/{d}{symbol_param}/x, where "name" is the model name, d is a string given by 'd'*time_deriv, and symbol_param is the symbol for the model parameters.

state_parameter_name()

str optas.models.Model.state_parameter_name	(		self,
		int	time_deriv
	)

Return the parameter name.

   @param time_deriv The time-deriviative required (i.e. position is 0, velocity is 1, etc.)
   @return The parameter name in the form {name}/{d}{symbol}/p, where "name" is the model name, d is a string given by 'd'*time_deriv, and symbol is the symbol for the model parameters.

Member Data Documentation

dim

optas.models.Model.dim

Model dimension.

dlim

optas.models.Model.dlim

Model limits.

name

optas.models.Model.name

The name of the model.

symbol

optas.models.Model.symbol

A short symbol to represent the model.

T

optas.models.Model.T

Number of time steps.

time_derivs

optas.models.Model.time_derivs

Time derivatives required for the model.

---

The documentation for this class was generated from the following file:

• models.py